알고리즘의 시간 복잡도를 알아보고자 합니다. Big O, Big Theta(Θ), Big Omega(Ω)의 차이점을 명확하게 이해하고, 다양한 알고리즘의 시간 복잡도 비교표를 통해 알고리즘 간 성능의 차이를 정리해볼 예정입니다.
목차
알고리즘 시간 복잡도 이해하기: Big O, Big Theta, Big Omega 설명
알고리즘의 시간 복잡도는 컴퓨터 프로그래밍과 데이터 구조에서 중요한 개념 중 하나입니다. 이는 알고리즘이 문제를 해결하기 위해 필요한 계산 작업의 양을 나타냅니다. 시간 복잡도를 이해하고 고려하는 것은 여러 가지 이유에서 중요합니다.
- 시간 복잡도는 알고리즘의 효율성을 평가하는 데 사용됩니다. 같은 문제를 해결하는 여러 알고리즘이 있을 때, 시간 복잡도를 기준으로 가장 효율적인 알고리즘을 선택할 수 있습니다.
- 소프트웨어의 성능을 최적화하고 사용자 경험을 향상시키는 데 중요한 역할을 합니다. 알고리즘의 실행 시간이 짧을수록 프로그램은 더 빠르게 작동하고, 이는 사용자가 보다 즉각적인 반응을 경험하게 합니다.
- 시간 복잡도는 컴퓨팅 자원의 효율적 사용과 직결됩니다. 자원이 제한된 환경에서는 최소한의 시간과 공간을 사용하여 최대한의 성능을 내는 알고리즘을 선택하는 것이 필수적입니다.
복잡도 표기법의 기본 개념
알고리즘의 시간 복잡도를 표현하기 위해 여러 가지 표기법이 사용됩니다. 가장 일반적으로 사용되는 표기법은 Big O 표기법입니다. Big O 표기법은 최악의 경우의 시간 복잡도를 나타내며, 알고리즘의 성능을 이해하는 데 중요한 도구입니다. 예를 들어, O(n)은 알고리즘의 실행 시간이 입력 크기 n에 비례하여 증가함을 의미합니다.
Big O 표기법 외에도 Big Theta(Θ)와 Big Omega(Ω) 표기법이 있습니다. Big Theta 표기법은 알고리즘의 평균적인 경우의 시간 복잡도를, Big Omega 표기법은 최선의 경우의 시간 복잡도를 나타냅니다. 이러한 표기법들은 알고리즘의 성능을 다각도에서 평가하고 비교하는 데 유용합니다.
알고리즘의 시간 복잡도를 정확하게 이해하고 적절한 표기법을 사용하는 것은 알고리즘을 선택하고 설계할 때 중요한 고려 사항입니다. 이러한 지식은 개발자가 보다 효율적이고 효과적인 소프트웨어 솔루션을 개발하는 데 도움을 줄 수 있습니다.
Big O 표기법
Big O 표기법은 알고리즘의 시간 복잡도를 나타내는 가장 흔하게 사용되는 방법입니다. 이 표기법은 알고리즘이 처리해야 할 데이터의 양이 증가할 때, 알고리즘의 실행 시간이 어떻게 증가하는지를 나타내는 데 초점을 맞춥니다. 즉, 입력 크기가 무한히 커질 때 알고리즘의 실행 시간이 어떻게 증가하는지를 설명합니다. Big O 표기법은 최악의 경우의 성능을 나타내므로, 알고리즘을 비교하고 선택하는 데 있어 중요한 기준점을 제공합니다.
자주 사용되는 Big O 예시

O(1) - 상수 시간
알고리즘의 실행 시간이 입력 크기에 관계없이 일정합니다. 예를 들어, 배열의 특정 인덱스에 있는 요소에 접근하는 연산은 항상 같은 시간이 걸립니다.
O(n) - 선형 시간
알고리즘의 실행 시간이 입력 크기에 비례하여 증가합니다. 예를 들어, 배열을 순회하며 각 요소를 한 번씩 확인하는 경우, 요소의 수(n)만큼 시간이 걸립니다.
O(log n) - 로그 시간
알고리즘의 실행 시간이 입력 크기의 로그에 비례하여 증가합니다. 이는 주로 분할 정복 알고리즘에서 볼 수 있으며, 예를 들어 이진 검색이 여기에 해당됩니다.
O(n^2) - 이차 시간
알고리즘의 실행 시간이 입력 크기의 제곱에 비례하여 증가합니다. 대표적인 예로는 버블 정렬이나 선택 정렬과 같은 간단한 정렬 알고리즘이 있습니다.
실제 코드 예시를 통한 설명
O(1) 예시: 배열에서 요소 접근

O(n) 예시: 선형 검색

O(log n) 예시: 이진 검색

O(n^2) 예시: 버블 정렬

Big Theta (Θ) 표기법
Big Theta (Θ) 표기법은 알고리즘의 시간 복잡도를 나타내는 또 다른 방법으로, 알고리즘의 평균적인 실행 시간을 표현합니다. Big Theta는 알고리즘이 실행될 때 소요되는 시간이 상한과 하한 사이에 존재함을 나타내며, 이는 입력 크기가 충분히 클 때, 알고리즘의 실행 시간이 특정 함수의 배수 내에 놓인다는 것을 의미합니다.
Big O와의 차이점
Big O와 Big Theta의 주된 차이점은 Big O가 알고리즘의 최악의 경우 실행 시간을 나타내는 데에 초점을 맞춘 반면, Big Theta는 알고리즘의 평균적인 실행 시간을 나타낸다는 점입니다.
사용 예시와 코드 설명
이진 검색 알고리즘은 정렬된 배열에서 특정 요소를 찾는 과정을 반으로 줄여가며 수행합니다. 이 알고리즘의 시간 복잡도는 O(log n)으로 잘 알려져 있으며, 이는 최악의 경우의 복잡도를 나타냅니다. 평균적으로 볼 때, 이진 검색의 시간 복잡도 역시 Θ(log n)으로 표현할 수 있습니다. 이는 입력 배열의 크기에 따라 실행 시간이 로그 증가하는 특성을 평균적으로도 보인다는 의미입니다.

위 코드에서 이진 검색은 배열의 중간 지점을 찾고, 타겟 값과 비교하여 검색 범위를 반으로 줄여 나갑니다. 최악의 경우, 타겟 값이 배열의 맨 끝에 위치하거나 배열에 없는 경우, 이 알고리즘의 실행 시간은 로그 함수에 비례하여 증가합니다. 그러나 평균적인 경우에도 실행 시간이 로그 함수에 비례한다는 점에서, 이진 검색의 시간 복잡도는 Θ(log n)으로 표현됩니다.
Big Omega (Ω) 표기법
Big Omega (Ω) 표기법은 알고리즘의 시간 복잡도를 나타내는 데 사용되며, 특히 알고리즘의 최선의 경우 성능을 설명할 때 사용됩니다. 이 표기법은 알고리즘의 실행 시간이 특정 함수의 값보다 크거나 같게 됨을 나타내는 데 사용되며, 알고리즘의 하한을 설정합니다. 즉, Ω 표기법은 알고리즘이 어떤 입력에 대해 최소한 얼마나 많은 시간이 소요될 것인지를 나타내는 데 초점을 맞춥니다.
Big O, Big Theta와의 비교
Big O, Big Theta, 그리고 Big Omega 표기법은 모두 알고리즘의 시간 복잡도를 설명하기 위해 사용되지만, 각각 다른 측면을 강조합니다.
- Big O (O): 알고리즘의 최악의 경우 실행 시간을 나타냅니다. 즉, 알고리즘이 처리해야 할 데이터의 양이 증가함에 따라 실행 시간이 어떻게 증가하는지의 상한선을 설정합니다. 이는 성능 평가의 보수적인 접근 방식으로, 알고리즘의 실행 시간이 이 기준을 초과하지 않음을 보장합니다.
- Big Theta (Θ): 알고리즘의 평균적인 경우 실행 시간을 나타냅니다. 이 표기법은 알고리즘의 실행 시간이 어떤 함수의 값에 근접하거나 일치함을 나타내며, 알고리즘의 평균적인 성능을 보여줍니다.
- Big Omega (Ω): 알고리즘의 최선의 경우 실행 시간을 나타냅니다. 이는 알고리즘의 성능이 특정 하한선보다 좋을 수 있음을 나타내며, 알고리즘이 얼마나 효율적일 수 있는지에 대한 통찰력을 제공합니다.
이러한 표기법들의 조합을 통해, 알고리즘의 성능을 다각도로 평가하고 이해할 수 있습니다. Big Omega 표기법은 특히 알고리즘이 어떤 조건에서는 예상보다 더 좋은 성능을 낼 수 있음을 보여주는 데 유용하며, 이를 통해 알고리즘의 최적화 가능성을 탐구할 수 있습니다.
알고리즘 시간 복잡도 비교표
비교표를 통해 알고리즘의 선택 시, 각 알고리즘의 성능 특성을 고려할 수 있으며, 특정 상황에 가장 적합한 알고리즘을 선택하는 데 도움이 됩니다. 예를 들어, 최악의 경우를 피하고자 할 때는 Big O 표기법을, 평균적인 성능이 중요할 때는 Big Theta를, 최선의 경우를 기대할 수 있는 상황에서는 Big Omega 표기법을 참고하면 됩니다.
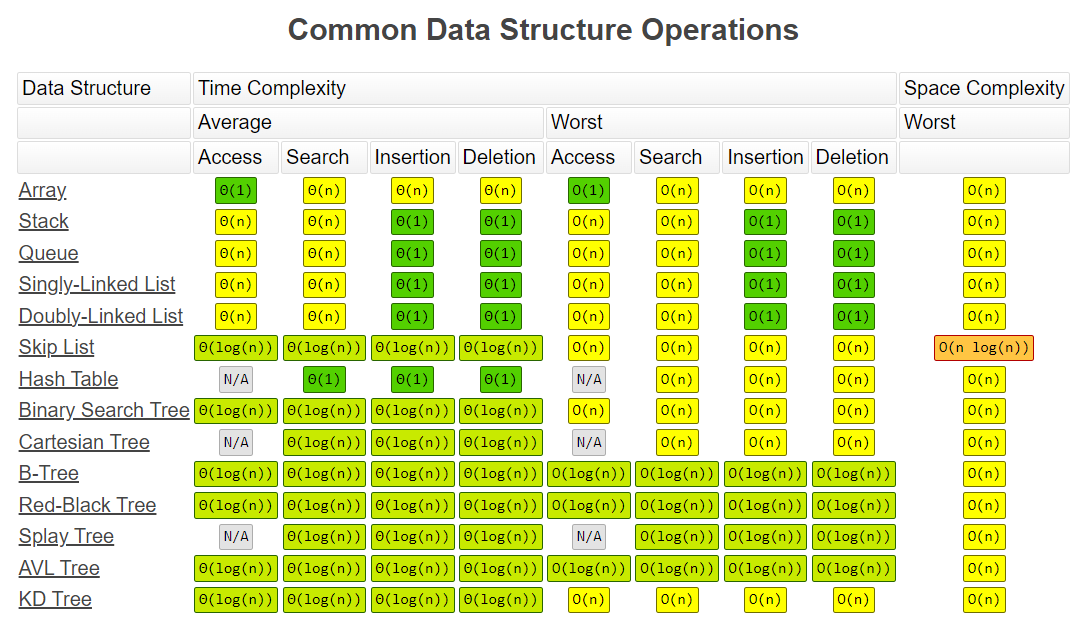
Common Data Structure Operations
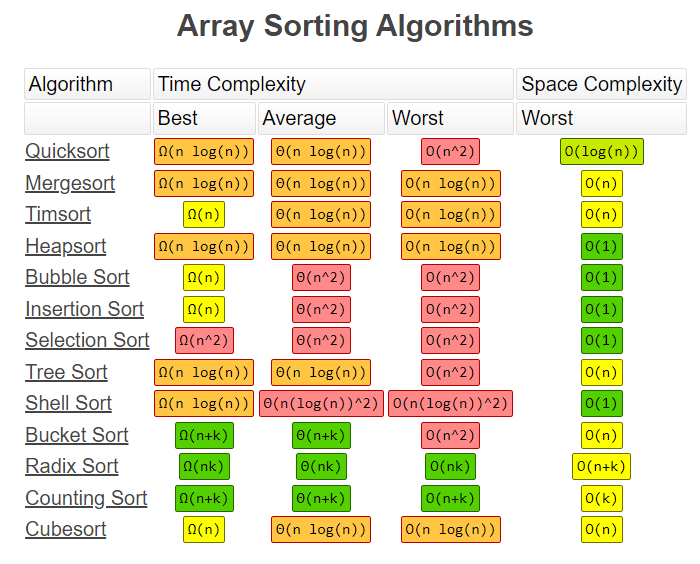
Arrary Sorting Algorithms
마무리
알고리즘의 시간 복잡도는 알고리즘 선택과 최적화 과정에서 필수적인 고려 사항입니다. 복잡도 분석은 주어진 문제에 대해 알고리즘의 실행 시간과 필요한 자원을 예측할 수 있게 해주며, 이는 효율적인 소프트웨어 개발의 핵심입니다. 알고리즘의 시간 복잡도를 이해함으로써, 개발자는 데이터의 크기와 구조에 따라 가장 적합한 알고리즘을 선택할 수 있으며, 이는 실행 시간의 단축, 자원 사용의 최적화, 그리고 결국 사용자 경험의 향상으로 이어집니다.
효율적인 알고리즘 선택의 중요성 강조
알고리즘의 효율성은 단순히 더 빠른 실행 시간을 의미하는 것이 아닙니다. 효율적인 알고리즘 선택은 시스템의 전반적인 성능을 향상시키고, 제한된 컴퓨팅 자원을 최적으로 활용하며, 확장성과 유지보수성을 높이는 데 기여합니다. 특히 대규모 데이터를 다루는 애플리케이션에서는, 알고리즘의 시간 복잡도가 시스템 성능에 결정적인 영향을 미칩니다.
Big O, Big Theta, Big Omega와 같은 복잡도 표기법을 이해하고 적절히 적용하는 것은, 알고리즘의 성능을 정확히 평가하고, 다양한 요구 사항과 제약 조건을 만족시키는 솔루션을 개발하는 데 있어 필수적입니다. 이러한 지식은 개발자가 보다 빠르고, 효율적이며, 확장 가능한 알고리즘을 설계하고 구현할 수 있도록 돕습니다.
'개발' 카테고리의 다른 글
| [최적화 및 문제풀이] 자연수 a³ + b³ = c³ + d³ 문제 (2) | 2024.08.31 |
|---|---|
| 배열 교집합 계산: 알고리즘 분석과 Big-O 시간 복잡도 (0) | 2024.08.30 |
| [Architecture] Architectural Tactics과 Architectural Style 차이점 (44) | 2024.03.18 |
| [논문 리뷰][Architecture] Foundations for the Study of Software Architecture (46) | 2024.03.12 |
| [Architecture] Architectural Style 이란? (2) | 2024.03.11 |

