Backpropagation(역전파)

Backpropagation(역전파)

역전파란 역방향으로 오차를 전파시키면서 각 층의 가중치를 업데이트하고 최적의 학습 결과를 찾아가는 것이다.

 

이를 도식화하면 아래와 같습니다.

오차역전파법

 

3번 제곱오차 $𝐶$를 구하는 방법은 다음과 같습니다.

Equation 1:

• $𝑧_1^2=𝑤_{11}^2 𝑥_1+𝑤_{12}^2 𝑥_2+…+𝑤_{112}^2 𝑥_{12}+𝑏_1^2$
• $𝑧_2^2=𝑤_{21}^2 𝑥_1+𝑤_{22}^2 𝑥_2+…+𝑤_{212}^2 𝑥_{12}+𝑏_2^2$
• $𝑧_3^2=𝑤_{31}^2 𝑥_1+𝑤_{32}^2 𝑥_2+…+𝑤_{312}^2 𝑥_{12}+𝑏_3^2$
• $𝑎_1^2=𝑎(𝑧_1^2), \; 𝑎_2^2=𝑎(𝑧_2^2), \; 𝑎_3^2=𝑎(𝑧_3^2)$

Equation 2:

• $𝑧_1^3=𝑤_{11}^3 𝑎_1^2+𝑤_{12}^3 𝑎_2^2+𝑤_{13}^2 𝑎_3^2+𝑏_1^3$
• $𝑧_2^3=𝑤_{21}^3 𝑎_1^2+𝑤_{22}^3 𝑎_2^2+𝑤_{23}^2 𝑎_3^2+𝑏_2^3$
• $𝑎_1^3=𝑎(𝑧_1^3), \; 𝑎_2^3=𝑎(𝑧_2^3)$

Equation 3:

• $C=\frac{1}{2} \{(𝑡_1−𝑎_1^3 )^2+(𝑡_2−𝑎_2^3 )^2 \}$

 

4번 오차역전파법으로 유닛의 오차 $𝜹$를 계산하는 것은 다음과 같습니다.

Equation 1:

• $𝛿_𝑗^𝐿=\frac{𝜕𝐶}{𝜕𝑎_𝑗^𝐿} 𝑎′(𝑧_𝑗^𝐿)$

Equation 2:

• $𝛿_𝑖^𝑙= \{𝛿_1^{𝑙+1} 𝑤_1𝑖^{𝑙+1}+𝛿_2^{𝑙+1} 𝑤_2𝑖^{𝑙+1}+…+𝛿_𝑚^{𝑙+1} 𝑤_{𝑚𝑖}^{𝑙+1} \} $
• $𝛿_𝑖^𝑙=\{𝛿_1^{𝑙+1} 𝑤_1𝑖^{𝑙+1}+𝛿_2^{𝑙+1} 𝑤_2𝑖^{𝑙+1}+…+𝛿_𝑚^{𝑙+1} 𝑤_{𝑚𝑖}^{𝑙+1} \} 𝑎^′ (𝑧_𝑖^𝑙 ) \qquad $(𝑙 𝑖𝑠 𝑎𝑛 𝑖𝑛𝑡𝑒𝑔𝑒𝑟 𝑡ℎ𝑎𝑛 𝑜𝑟 𝑒𝑞𝑢𝑎𝑙 𝑡𝑜 2)

 

5번 $𝛿$ 에서 제곱오차 $𝐶$의 편미분을 계산하는 것은 다음과 같습니다.

Equation 1:

• $\frac{𝜕𝐶}{𝜕𝑤_{𝑗𝑖}^𝑙}=𝛿_𝑗^𝑙 𝑎_𝑖^{𝑙−1}, \quad \frac{𝜕𝐶}{𝜕𝑏_𝑗^𝑙}=𝛿_𝑗^𝑙 \qquad (𝑙=2, 3,…)$

 

6번 비용함수 $𝑪_𝑻$  와 기울기 $𝜵𝑪_𝑻$  를 계산하는 것은 다음과 같습니다.

Equation 1:

• $𝐶_𝑇=𝐶_1+𝐶_2+… 𝐶_64$

 

7번 경사하강법을 사용해 가중치와 편향을 계산하는 것은 다음과 같습니다.

Equation 1:

• $(∆𝑤_{11}^2,…,∆𝑤_{11}^3,…,∆𝑏_1^2,…,∆𝑏_1^3,…)=−𝜂\left( \frac{ 𝜕𝐶_𝑇}{𝜕𝑤_{11}^2},…,\frac{𝜕𝐶_𝑇}{𝜕𝑤_{11}^3},…,\frac{𝜕𝐶_𝑇}{𝜕𝑏_1^2},…,\frac{𝜕𝐶_𝑇}{𝜕𝑏_1^3},…\right)$
• $(𝑤_{11}^2+∆𝑤_{11}^2,…,𝑤_{11}^3+∆𝑤_{11}^3,…,𝑏_1^2+∆𝑏_1^2,…,𝑏_1^3+∆𝑏_1^3,…)$

 

위 내용을 정리하면 다음과 같습니다.

Prepare training data. Set the initial value of each unit's weight and bias. The initial value is usually a normally distributed random number. Also set the learning rate $𝜂$ to be a positive constant with a reasonably small value. Calculate the output value of the unit and the squared error $𝐶$ . Calculate the weighted input $𝑧$, the activation function value $𝑎$. It also computes the squared error $𝐶$. The error $𝛿$ of each layer unit is calculated using the error backpropagation method. Calculate the error $d$ of the output layer unit using Equation 1. Then, using Equation 2, the error d of the hidden layer unit is calculated. Calculate the partial derivative of the squared error $𝐶$ from the error in units. Calculate the partial derivative of the weight and bias of the squared error $𝐶$ using the unit error $𝛿$ calculated in step 4 and Equation 3. Compute the cost function $𝐶_𝑇$ and its slope $∇𝐶_𝑇$. After adding the results of 3 to 5 to all data, add them all together to obtain the cost function $𝐶_𝑇$ and its slope $∇𝐶_𝑇$. Update the weight and bias values with the gradient obtained in step 6. Update weights and bias values using gradient descent. Repeat 3-7. Repeat calculations 3 to 7 until it is determined that the cost function $𝐶_𝑇$ is small enough.

위 알고리즘에서 사용된 Equation 1, 2, 3은 아래와 같습니다.

Equation

 

다음은 위 알고리즘에서 사용된 수식을 이해가 위한 자료입니다.

유닛의 오차 $𝛿_𝑗^𝑙 $ 구하기

유닛의 오차

 

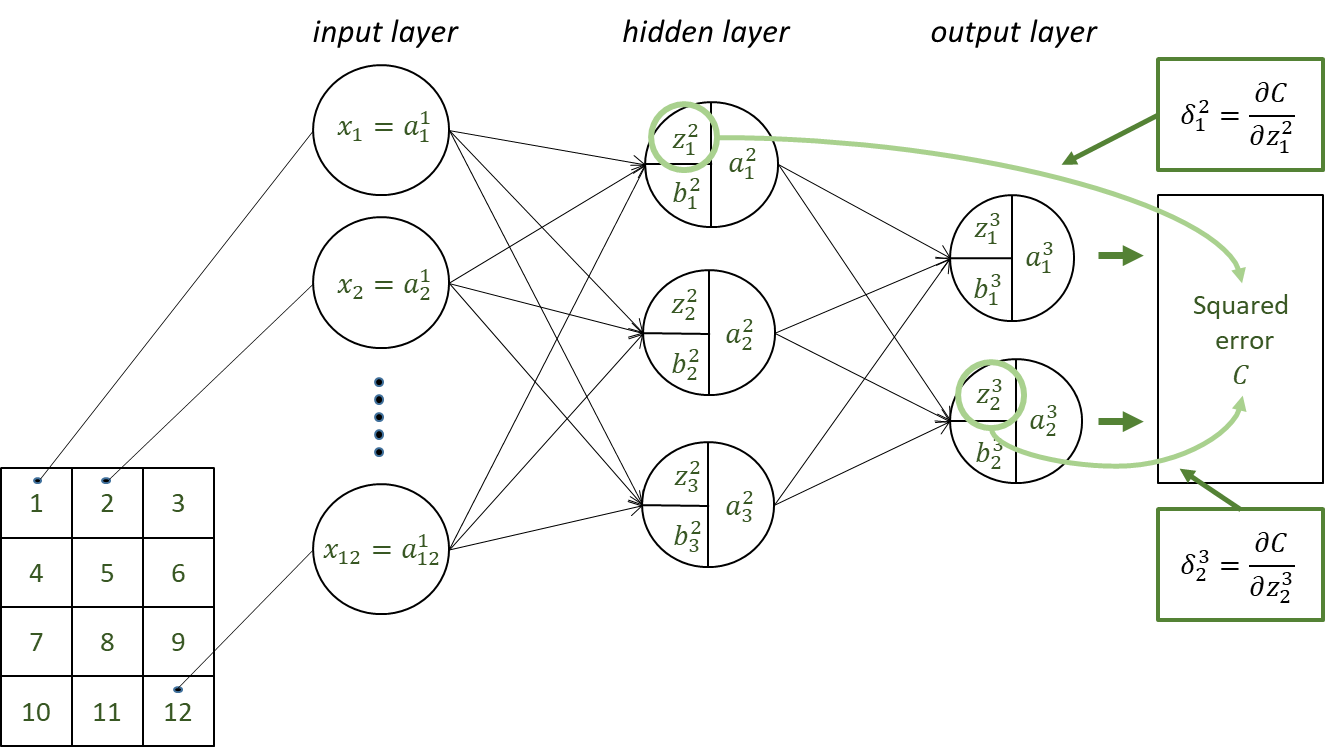
유닛의 오차 $ 𝛿_𝑗^𝑙 $

$$𝛿_𝑗^𝑙=\frac{𝜕𝐶}{𝜕𝑧_𝑗^𝑙}\quad(𝑙=2,3,…)$$

Squared error $𝐶$

$$C=\frac{1}{2} \{(𝑡_1−𝑎_1^3 )^2+(𝑡_2−𝑎_2^3 )^2 \}$$

$𝛿_1^2$, $𝛿_2^3$ 은 다음과 같습니다.

$$𝛿_1^2=\frac{𝜕𝐶}{𝜕𝑧_1^2}, \qquad 𝛿_2^3=\frac{𝜕𝐶}{𝜕𝑧_2^3}$$

 

제곱오차 $𝐶$의 편미분을 구하고, $𝛿_𝑗^𝑙$로 표현하기

$\frac{𝜕𝐶}{𝜕𝑤_{11}^2}$ 를 $𝛿_𝑗^𝑙$로 표현하기

Squared error C #1

 

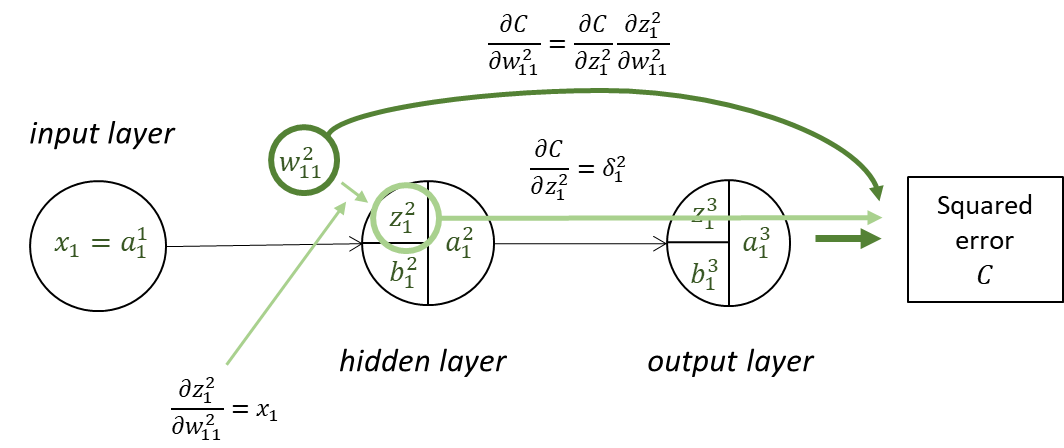
$\frac{𝜕𝐶}{𝜕𝑤_{11}^2}=\frac{𝜕𝐶}{𝜕𝑧_1^2}\frac{𝜕𝑧_1^2}{𝜕𝑤_{11}^2} \qquad \left(\frac{𝜕𝑧_1^2}{𝜕𝑤_{11}^2}=𝑥_1, \quad \frac{𝜕𝐶}{𝜕𝑧_1^2}=𝛿_1^2\right)$

$\frac{𝜕𝐶}{𝜕𝑤_{11}^2}=𝛿_1^2 𝑥_1=𝛿_1^2 𝑎_1^1$

 

$\frac{𝜕𝐶}{𝜕𝑤_{11}^3}$ 를 $𝛿_𝑗^𝑙$로 표현하기

Squared error C #2

 

$\frac{𝜕𝐶}{𝜕𝑤_{11}^3}=\frac{𝜕𝐶}{𝜕𝑧_1^3} \frac{𝜕𝑧_1^3}{𝜕𝑤_{11}^3} \qquad \left(\frac{𝜕𝑧_1^3}{𝜕𝑤_{11}^3}=𝑎_1^2, \quad \frac{𝜕𝐶}{𝜕𝑧_1^3}=𝛿_1^3 \right)$

$\frac{𝜕𝐶}{𝜕𝑤_{11}^3}=𝛿_1^3 𝑎_1^2$

 

$\frac{𝜕𝐶}{𝜕𝑏_1^2}$ 를 $𝛿_𝑗^𝑙$로 표현하기

Squared error C #3

 

$\frac{𝜕𝐶}{𝜕𝑏_1^2}=\frac{𝜕𝐶}{𝜕𝑧_1^2} \frac{𝜕𝑧_1^2}{𝜕𝑏_1^2}=𝛿_1^2 \qquad \left(\frac{𝜕𝑧_1^2}{𝜕𝑏_1^2}=1, \quad \frac{𝜕𝐶}{𝜕𝑧_1^2}=𝛿_1^2 \right)$

 

$\frac{𝜕𝐶}{𝜕𝑏_1^3}$ 를 $𝛿_𝑗^𝑙$로 표현하기

Squared error C #4

 

$\frac{𝜕𝐶}{𝜕𝑏_1^3}=\frac{𝜕𝐶}{𝜕𝑧_1^3} \frac{𝜕𝑧_1^3}{𝜕𝑏_1^3}=𝛿_1^3 \qquad \left(\frac{𝜕𝑧_1^3}{𝜕𝑏_1^3}=1, \quad \frac{𝜕𝐶}{𝜕𝑧_1^3}=𝛿_1^3 \right)$

 

$𝛿_𝑗^𝑙 $를 사용하여 일반화

$\frac{𝜕𝐶}{𝜕𝑤_{𝑗𝑖}^𝑙}=𝛿_𝑗^𝑙 𝑎_𝑖^{𝑙−1}, \quad \frac{𝜕𝐶}{𝜕𝑏_𝑗^𝑙}=𝛿_𝑗^𝑙 \qquad (𝑙=2,3,…)$

 

출력 레이어의 $𝛿_𝑗^𝑙 $를 계산하기

Squared error C #5

 

$𝛿_𝑗^3=\frac{𝜕𝐶}{𝜕𝑧_𝑗^3}=\frac{𝜕𝐶}{𝜕𝑎_𝑗^3}  \frac{𝜕𝑎_𝑗^3}{𝜕𝑧_𝑗^3}=\frac{𝜕𝐶}{𝜕𝑎_𝑗^3} 𝑎^′ (𝑧_𝑗^3 )$

$𝛿_𝑗^𝐿=\frac{𝜕𝐶}{𝜕𝑎_𝑗^𝐿} 𝑎′(𝑧_𝑗^𝐿)$

 

히든 레이어의 $𝛿_𝑗^𝑙 $의 역점화(reverse ignition)

$𝛿_1^2=\frac{𝜕𝐶}{𝜕𝑧_1^2}=\frac{𝜕𝐶}{𝜕𝑧_1^3} \frac{𝜕𝑧_1^3}{𝜕𝑎_1^2} \frac{𝜕𝑎_1^2}{𝜕𝑧_1^2}+\frac{𝜕𝐶}{𝜕𝑧_2^3} \frac{𝜕𝑧_2^3}{𝜕𝑎_1^2} \frac{𝜕𝑎_1^2}{𝜕𝑧_1^2}$
$\frac{𝜕𝐶}{𝜕𝑧_1^3}=𝛿_1^3, \quad \frac{𝜕𝐶}{𝜕𝑧_2^3}=𝛿_2^3, \quad \frac{𝜕𝑧_1^3}{𝜕𝑎_1^2}=𝑤_{11}^3, \quad \frac{𝜕𝑧_2^3}{𝜕𝑎_1^2}=𝑤_{21}^3$
$\frac{𝜕𝑎_1^2}{𝜕𝑧_1^2}=𝑎^′ (𝑧_1^2 )$
$𝛿_1^2=𝛿_1^3 𝑤_{11}^3 𝑎^′ (𝑧_1^2 )+𝛿_2^3 𝑤_{21}^3 𝑎^′ (𝑧_1^2 )$

 

히든 레이어의 $𝛿_𝑗^𝑙 $의 역점화(reverse ignition) 일반화

$𝛿_𝑖^𝑙=\{𝛿_1^{𝑙+1} 𝑤_1𝑖^{𝑙+1}+𝛿_2^{𝑙+1} 𝑤_2𝑖^{𝑙+1}+…+𝛿_𝑚^{𝑙+1} 𝑤_{𝑚𝑖}^{𝑙+1} \} 𝑎^′ (𝑧_𝑖^𝑙 ) \qquad $ (𝑙 𝑖𝑠 𝑎𝑛 𝑖𝑛𝑡𝑒𝑔𝑒𝑟 𝑡ℎ𝑎𝑛 𝑜𝑟 𝑒𝑞𝑢𝑎𝑙 𝑡𝑜 2)