Activation Function (활성화 함수)
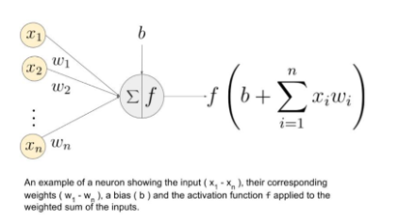
활성화 함수는 인공 신경망에서 입력 신호의 가중치 합을 출력 신호로 변환하는 함수입니다. 즉, artificial neuron들이 활성(fire)되는 빈도를 결정하는 임계값을 설정합니다.
활성화 함수의 주요 기능은 다음과 같습니다.
- 입력 신호의 가중치 합을 출력 신호로 변환
- 입력에 대한 비선형 변환을 통해 신경망의 표현력을 향상
- 역전파 알고리즘을 통해 신경망의 가중치를 학습
활성화 함수는 인공 신경망의 성능을 좌우하는 중요한 역할을 합니다.
활성화 함수는 크게 2가지로 나눌 수 있습니다.
- 선형 활성화 함수 (Linear activation function)
- 비선형 활성화 함수 (Non-linear activation function)
아래에서 선형 활성화 함수에 대해 간단히 설명하고, 비선형 활성화 함수는 선형 활성화 함수가 가지는 문제점을 어떻게 극복하는 알아보겠습니다.
Linear Activation Function (선형 활성화 함수)

- 선형 활성화 함수의 형태
$$ 𝐴=𝑐𝑥 $$ - 선형 활성화 함수의 특징
- 기울기가 항상 일정함
- 출력값의 범위가 입력값의 범위와 같음
- 입력값의 형태를 바꾸지 않음
- 문제점
- 역전파(경사 하강)를 사용하여 모델을 훈련할 수 없음
함수의 미분은 상수이며 입력인 X와 관계가 없습니다. 그래서 입력 뉴런의 어떤 가중치가 더 나은 예측을 제공할 수 있는지 되돌아가서 파악할 수 없습니다. - 신경망의 모든 레이어가 하나로축소됨
선형 활성화 함수를 사용하면 신경망의 레이어 수에 상관없이 마지막 레이어는 첫 번째 레이어의 선형 함수가 됩니다(선형 함수의 선형 조합은 여전히 선형 함수이기 때문입니다). 따라서 선형 활성화 함수는 신경망을 단 하나의 레이어로 만듭니다.
- 역전파(경사 하강)를 사용하여 모델을 훈련할 수 없음
Non-Linear Activation Function (비선형 활성화 함수)
비선형 활성화 함수는 입력값의 형태를 바꾸어 줌으로써, 선형 활성화 함수가 가지고 있던 문제점들을 해결할 수 있었습니다.
- 비선형 함수는 선형 활성화 함수의 문제점을 해결합니다.
- 비선형 함수는 입력과 관련된 파생 함수를 가지고 있기 때문에 역전파를 허용합니다.
- 선형 함수는 여러 층의 뉴런을 'stacking'하여 심층 신경망을 만들 수 있습니다. 복잡한 데이터 세트를 높은 수준의 정확도로 학습하려면 여러 개의 숨겨진 뉴런 레이어가 필요합니다.
- 비선형 활성화 함수의 유형
- Sigmoid activation function
- Hyperbolic tangent function
- ReLU (Rectified Linear Unit) function
- Leaky ReLU function
- Parametric ReLU
- Softmax
- Swish
이제부터 비선형 활성화 함수에 대해 하나씩 알아보겠습니다.
Sigmoid activation function

수식
$$ S(x)=\frac{1}{1+e^{-x}} $$
장점
- The function is monotonic.
- Smooth gradient
- 출력 값이 0과 1 사이로 바인딩되어, 각 뉴런의 출력을 정규화함
단점
- Vanishing gradient
- 0 중심이 아닌 출력 (Outputs not zero centered)
- 계산 비용이 많이 듦
Hyperbolic Tangent Function

수식
$$ f(x)=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} $$
장점
- 0 을 중심으로 출력, (-1, +1)
- 미분이 더 가파름
(Derivative is more steep, which means that it will be more efficient because it has a wider range for faster learning and grading.)
단점
- Sigmoid activation function 함수와 비슷한 단점있음
ReLU (Rectified Linear Unit) Function

수식
$$ f(x)=\left\{\begin{matrix}0, & for\ x \leq 0 \\1, & for\ x > 0 \\ \end{matrix}\right. $$
장점
- 계산 효율 - ReLU의 값은 [0, + 무한대]입니다
: 음수 축의 값이 0이라는 것은 네트워크가 더 빠르게 실행된다는 것을 의미합니다. 계산 부하가 sigmoid function 및 hyperbolic tangent funtions보다 적기 때문에 다층 네트워크에 대한 선호도가 높습니다. - 비선형 (non-linear)
단점
- Dying ReLU 문제
: 입력이 0에 가까워지거나 음수일 때 함수의 기울기가 0이 되면 네트워크는 역전파(backpropagation)를 수행할 수 없고 학습할 수 없습니다.
Leaky ReLU Function

수식
$$ f(x)=\left\{\begin{matrix}0.01x, & for\ x < 0 \\x, & for\ x \geq 0 \\ \end{matrix}\right. $$
장점
- Dying ReLU 문제 방지
: 이 변형 ReLU는 음수 영역에서 작은 양의 기울기를 가지므로 음수 입력값에 대해서도 역전파가 가능합니다. - 다른 장점들은 ReLU와 같습니다.
단점
- 결과가 일관적이지 않습니다
: Leaky ReLU는 음수 입력 값에 대해 일관된 예측을 제공하지 않습니다.
Parametric ReLU Function

수식
$$ f(x)=\left\{\begin{matrix}\alpha x, & for\ x < 0 \\x, & for\ x \geq 0 \\ \end{matrix}\right. $$
장점
- 음의 기울기(negative slope)를 학습할 수 있습니다.
: Leaky ReLU와 달리 이 함수는 함수의 음수 부분의 기울기를 인수로 제공합니다. 따라서 역전파를 수행하여 α의 가장 적절한 값을 학습할 수 있습니다. - 다른 장점들은 ReLU와 같습니다.
단점
- 문제마다 다른 성능을 보일 수 있습니다.
Softmax Function

수식
$$ \text{Softmax}(x_{i}) = \frac{\exp(x_i)}{\sum_j \exp(x_j)} $$
장점
- 다른 활성화 함수에서 하나의 클래스만 처리할 수 있지만, Softmax 함수는 여러 클래스를 처리할 수 있습니다.
- 출력 뉴런에 유용합니다
: 일반적으로 SoftMax는 입력을 여러 범주로 분류해야 하는 신경망의 출력 레이어에서 사용됩니다.
Sigmoid 와 Softmax 비교
Sigmoid 함수의 그래프와 Softmax 함수의 그래프 사이에는 큰 차이가 없지만, 다음과 같은 차이를 가지고 있습니다.
| Sigmoid Function | Softmax Function |
| logistic regression model 에서 binary classification 에 사용됨 | logistic regression model 에서 multi-classification 에 사용됨 |
| 확률 합이 1 일 필요는 없음 | 확률 합이 1 |
| 신경망의 여러 레이어에서 사용됨 | 신경망을 구축하는 동안 activation function 으로 사용됨 |
| 높은 값은 다른 값보다 높은 확률을 가짐 | 높은 값은 높은 확률을 갖지만, 더 높은 확률은 아님 |
Swish Function

수식
$$ f(x) = \frac{x}{1 + e^{-x}} $$
Swish는 Google의 연구원들이 발견한 새로운 self-gated activation function
- ReLU와의 가장 중요한 차이점은 음의 영역에 있습니다. 입력이 증가해도 swish function의 출력은 떨어질 수 있습니다. 이것은 흥미롭고 swish 만의 특징입니다.
https://arxiv.org/abs/1710.05941v1
Swish: a Self-Gated Activation Function
The choice of activation functions in deep networks has a significant effect on the training dynamics and task performance. Currently, the most successful and widely-used activation function is the Rectified Linear Unit (ReLU). Although various alternative
arxiv.org
'개발 > DNN' 카테고리의 다른 글
| Backpropagation(역전파) (0) | 2023.10.08 |
|---|---|
| Gradient Descent Method(경사하강법) (0) | 2023.09.19 |
| Learning(학습)이란? (0) | 2023.09.18 |
| Cost Function(비용 함수) (0) | 2023.09.17 |
| Perceptron (0) | 2023.09.02 |



