[수학][오답노트] 성대 경시 27회

성대 경시 문제 중 틀린 문제를 다시 풀때 어려워했던 내용에 대해 정리하기 위한 글로 한 회차를 다 풀때마다 정리할 예정입니다.

 

오답 노트

이번은 27회차를 정리합니다.

 

오답 문제 - 1

이 문제는 이전 블로그에서 정리했던 내용 중 하나로 여기에서는 성대 경시 문제만 따로 정리해놓겠습니다.

[수학][오답 노트] 피보나치 수열

 

 

다음과 같이 수가 어떤 규칙에 따라 나열되어 있습니다. □ 안에 알맞은 수는 얼마입니까?

오답 문제 - 1

 

 

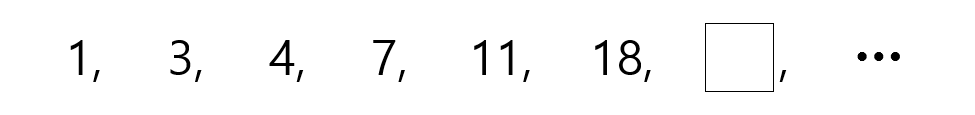
피보나치 수열 규칙을 대입해보면 아래와 같이 29 가 됨을 확인할 수 있습니다.

오답 문제 - 1 풀이

 

 

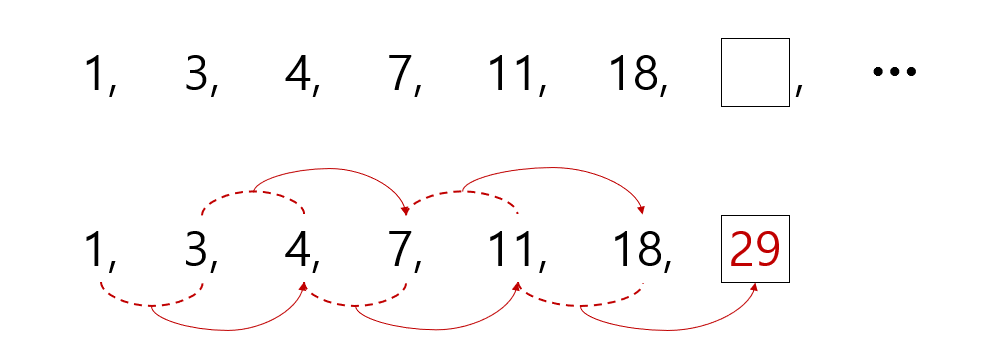
오답 문제 - 2

〈보기〉는 각 가로줄과 세로줄에 1, 2, 3이 한 개씩 있고, 굵은 선 안에도 1, 2, 3이 한 개씩 있습니다. 다음 오른쪽 그림에 〈보기〉와 같이 각 가로줄과 세로줄에 1, 2, 3, 4가 한 개씩 있고, 굵은 선 안에도 1, 2, 3, 4가 한 개씩 있도록 수를 써넣을 때, 세자리 수 ㉠㉡㉢은 무엇입니까?

오답 문제 - 2

 

 

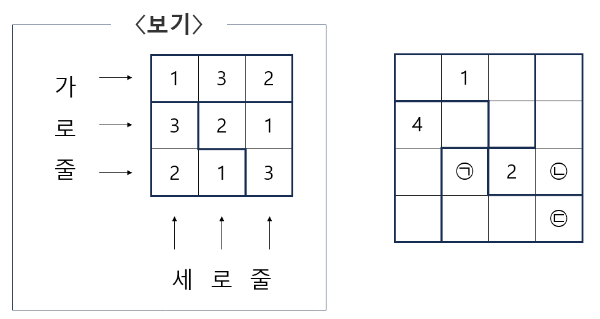
문제를 풀기 위해 위에 노란음영 규칙들을 잘 기억하고,  먼저 1의 위치를 찾아보겠습니다.

 

〈규칙 1〉 가로줄과 세로줄에 1, 2, 3, 4가 하나씩 있어야 한다는 규칙에 의해 1이 들어갈 수 없는 자리에 X 표시를 하면 아래와 같습니다.

규칙 1에 의한 X 표시

 

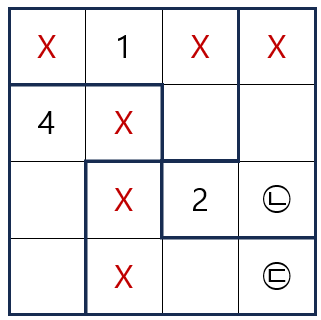
여기까지는 1이 확실히 들어갈 수 있는 자리를 찾을 수 없습니다. 여기에 〈규칙 2〉 굵은 선 안에도 1, 2, 3, 4가 하나씩 있어야 한다는 규칙을 적용해보겠습니다.

규칙 2에 의한 X 표시

 

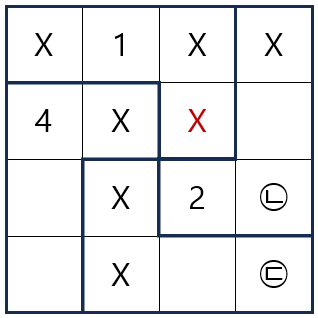
규칙 2까지 적용하면 1이 들어갈 수 있는 자리를 발견할 수 있습니다.

규칙 1, 2에 의해 발견한 1이 들어가는 자리

 

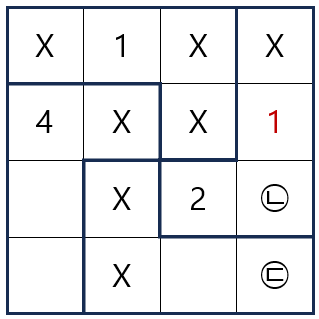
새로운 1일 추가됨으로 규칙 1, 2를 다시 적용해볼 수 있습니다.

규칙 1, 2를 적용

 

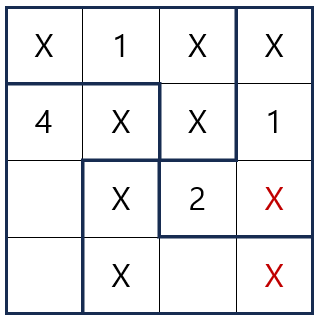
위 그림에서 규칙 1 중 세로줄에는 1, 2, 3, 4가 하나씩 있어야 한다는 규칙에 의해 1이 들어갈 수 있는 자리를 추가로 찾을 수 있습니다.

새로 찾은 1이 들어갈 자리

 

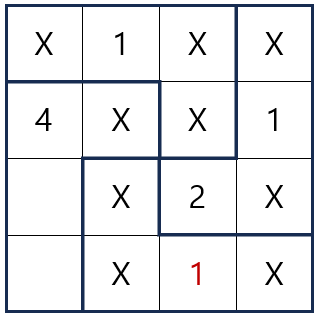
위 그림에서 규칙 1, 2를 적용해서 1이 들어갈 수 없는 자리를 찾으면 마지막 1이 들어갈 수 있는 자리까지 확인할 수 있습니다.

마지막 1이 들어갈 자리

 

 

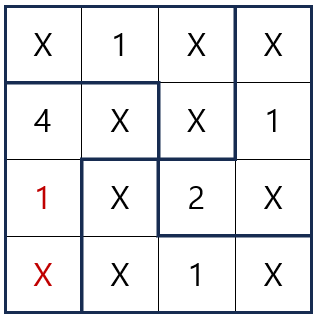
이와 같은 방법으로 2가 들어갈 수 있는 자리를 찾으면 다음과 같고, ㉢ 이 2가 됨을 알 수 있습니다.

2가 들어가는 자리들

 

 

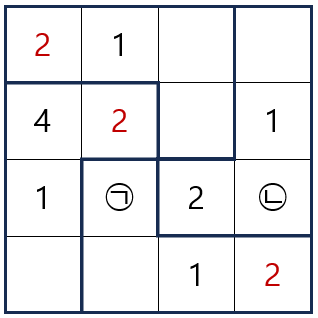
다음으로 3이 들어가는 자리를 찾으면 다음과 같고, ㉠ 이 3이 됨을 알 수 있습니다.

3이 들어가는 자리들

 

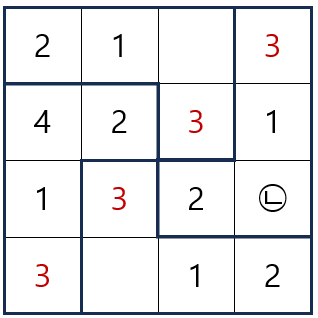
최종적으로 ㉠㉡㉢ 은 342가 됨을 알 수 있습니다.

 

오답 문제 - 3

아래 그림은 6칸씩 6줄인 표에 어떤 규칙에 따라 ○와 △를 그린 것입니다. 같은 규칙으로 12칸씩 12줄인 표에 ○와 △를 그릴 때, ○는 모두 몇 개입니까?

오답 문제 - 3

 

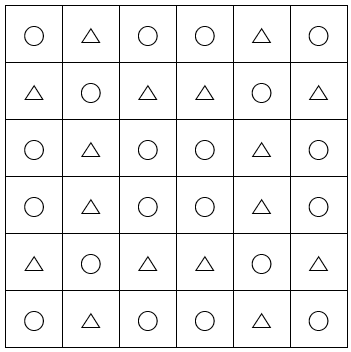
아래와 같이 9개의 칸을 묶어보면 규칙이 보입니다.

오답 문제 - 3 규칙

 

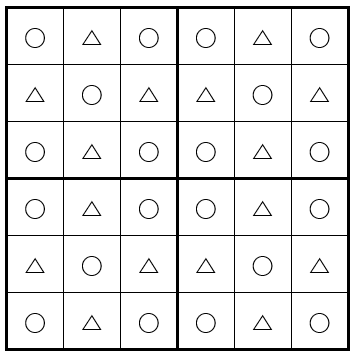
이를 12칸씩 12줄로 확장해보면 다음과 같습니다.

12칸씩 12줄

 

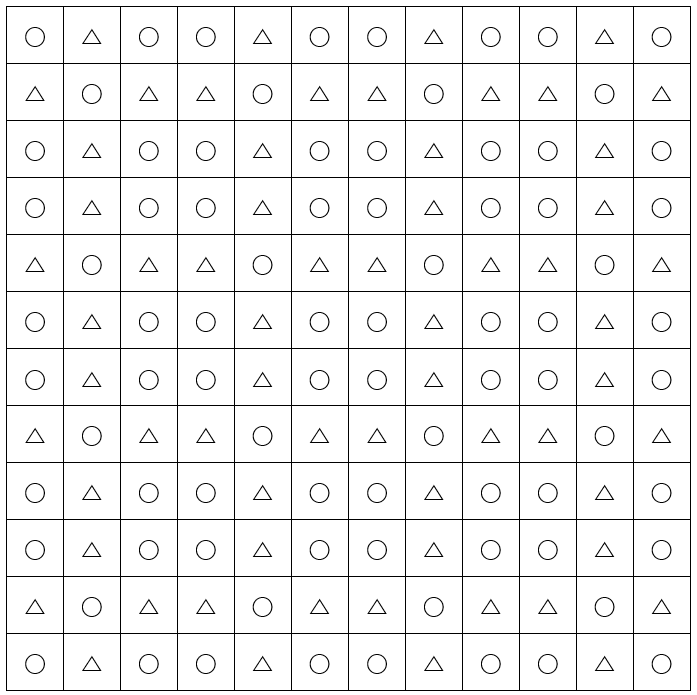
○는 모두 80 개 입니다.

9개칸을 묶은 규칙(○이 5개)이 16번 반복되는 것으로 5×16＝80 으로 계산할 수도 있습니다.

 

오답 문제 - 4

난주가 생각하고 있는 세 자리 수를 다른 학생들이 찾으려고 합니다. 학생이 세 자리 수를 쓰면 난주는 그 수 옆에 □와 △를 씁니다. □는 난주가 생각하고 있는 수와 같은 자리에, △는 다른 자리에 숫자가 있다는 기호입니다. 〈보기〉를 들면 다음과 같습니다.

오답 문제 - 4 보기

 

여기에서 □는 숫자 3을, △는 숫자 2를 나타냅니다. 세 학생이 쓴 수 옆에 난주가 다음과 같이 기호를 썼다면 난주가 생각하고 있는 수는 무엇입니까?

오답 문제 - 4

 

 

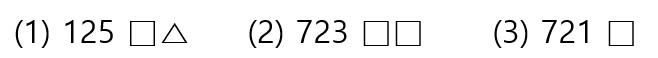
이 문제를 어려워했던 포인트는 〈보기〉에서 난주가 쓴 기호에 숫자의 위치가 나타난다고 생각했던 부분이었습니다. □와 △는 일의 자리, 십의 자리, 백의 자리 위치를 나타내는 것이 아니라는 것을 이해하고 난 이후 문제를 풀 수 있었습니다.

 

난주가 생각하는 수를 구하기 위해 난주가 생각하는 수와 같은 자리에 있는 수가 제일 많은 (2)에서 난주가 생각하는 숫자를 3개 (ⓐ, ⓑ, ⓒ) 생각해볼 수 있습니다.

(2)를 통해 유추할 수 있는 수

 

난주가 생각한 수 ⓐ, ⓑ, ⓒ 각각을 (3) 721에 적용하여 기호를 그려보면 다음과 같습니다.

난주가 생각한 수와 721 를 비교하여 기호를 그려본 경우

 

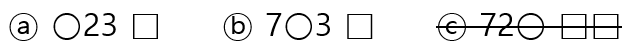
ⓒ 는 안 되는 것을 알 수 있습니다.

이제 난주가 생각한 수 ⓐ, ⓑ 각각을 (1) 125에 적용하여 기호를 그려보겠습니다.

난주가 생각한 수와 125를 비교하여 기호를 그려본 경우

 

ⓑ 는 125와 비교하여 □△을 만들 수 없는 것을 알 수 있습니다.

 

ⓐ 는 ○를 제외하고 □ 하나를 그릴 수 있습니다. 

□ 가 나온 이유

 

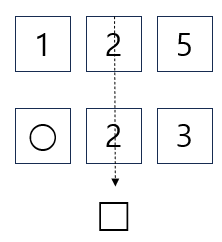
○에 어떤 수를 채워 125와 비교했을 때 △ 기호를 하나 더 만들 수 있으면 됩니다. 그럼 ○에는 125 중에 포함된 숫자이어야 하기 때문에 2를 제외한 1 또는 5의 숫자가 들어갈 수 있습니다.

○에 1 또는 5를 대입해본 경우

 

 

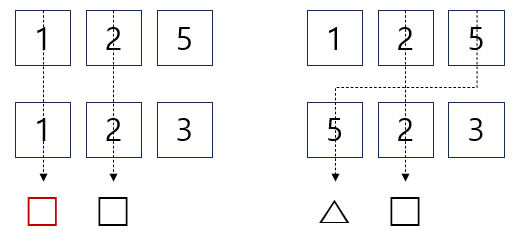
난주가 생각한 수는 523 임을 알 수 있습니다.

 

 

 

아이 교육에 대해 관심 있으신 분들은 편하게 연락 또는 댓글 달아주세요.