성대 경시 문제 중 틀린 문제를 다시 풀때 어려워했던 내용에 대해 정리하는 오답노트입니다.
목차
정리
이번은 29회차를 정리합니다.
1. 문제
오른쪽 그림에서 가로와 세로 방향으로 놓인 세 수의 합이 모두 0 또는 2가 되도록 빈칸에 수를 넣으려고 합니다. 완성된 그림은 모두 몇 개입니까?
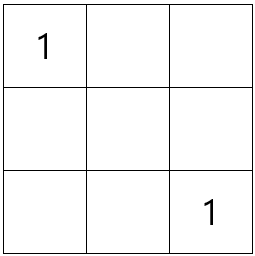
이 문제를 풀기 위해서 맨 윗줄의 합이 2가 되는 경우는 아래와 같이 2가지 경우(①)가 있습니다. 맨 상단 좌측에 1이 있기 때문에 0은 될 수 없습니다.
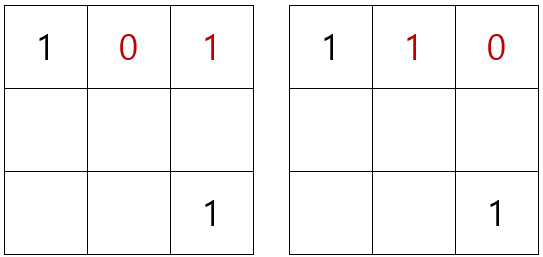
첫 번째 경우를 살펴보면 2번째 줄 오른쪽은 세로의 합이 0 또는 2가 된다는 규칙에 의해 0으로 채워지는 것을 알 수 있습니다.
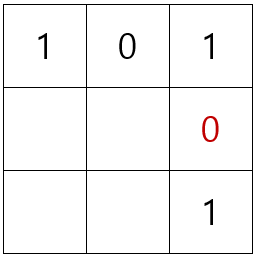
그럼 마지막 세번째 줄의 합은 0이 될 수 없으므로, 2가 되는 경우를 찾아보면 아래와 같이 2가지 경우(②)가 나오게 됩니다.
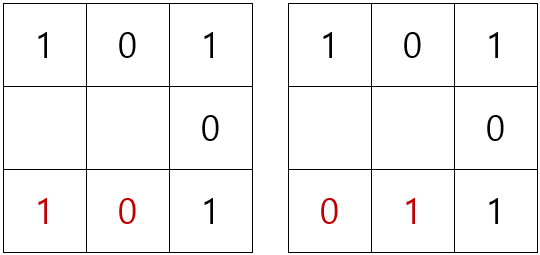
위의 경우에서 첫번째 경우를 먼저 생각하면 아래와 같이 그림이 완성될 수 있습니다.
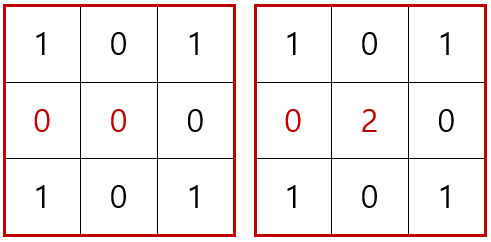
②의 첫 번째 경우를 따져보았으니, 이번에는 ②의 두 번째 경우를 생각해보겠습니다.
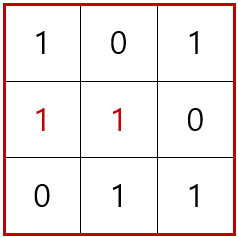
②에서 2가지 경우를 따져서 완성된 그림 3가지를 찾을 수 있습니다. 그런데 ①의 경우에서 두 번째 경우를 아직 확인하지 않았습니다. ①의 경우에서 두 번째 경우에서 두 번째 줄 오른쪽은 세로의 합은 0 또는 2가 된다는 규칙에 의해 1이 됩니다.
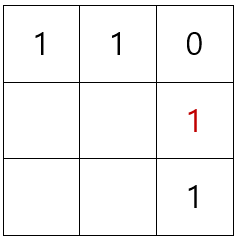
이때 두 번째 줄을 채울 수 있는 방법은 아래와 같이 2가지 경우(③)가 됩니다.
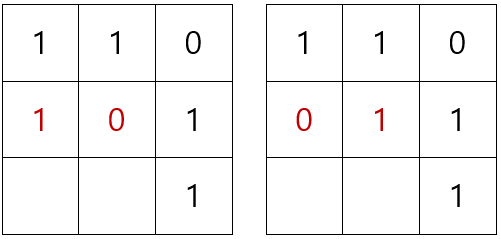
③의 경우에서 첫 번째 경우를 먼저 생각해보겠습니다.
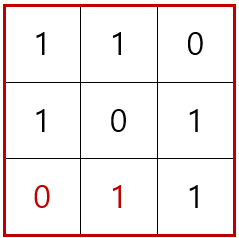
다음으로는 ③의 경우에서 두 번째 경우를 생각해보겠습니다.
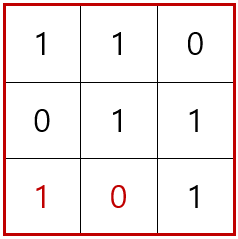
이로써 모든 경우를 다 생각보았습니다. 완성된 그림은 총 5가지 입니다.
어려웠던 포인트
이 문제의 규칙은 세로, 가로의 합이 0 또는 2라는 것만 주어졌지만, 문제를 풀면서 숫자는 0 또는 1만 쓴다는 규칙을 스스로 만들어내어 아래와 같이 가운데 2가 들어가는 경우를 찾지 못 해 문제 푸는데 어려웠했습니다.
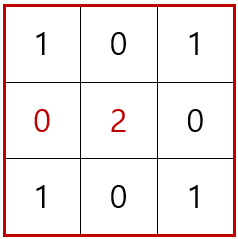
2. 문제
각 자리 숫자의 합이 14인 세 자리 수 중에서 백과 십의 자리 숫자의 차가 일의 자리 숫자와 같은 세 자리 수는 모두 몇 개입니까?
먼저, 아래와 같이 임의의 세 자리 수를 ㉠㉡㉢으로 놓습니다.

그럼 각 자리 숫자의 합이 14라는 조건에 의해 아래와 같은 식 (①) 이 나올 수 있습니다.
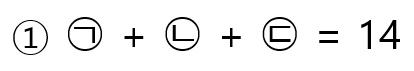
백과 십의 자리 숫자의 차가 일의 자리 숫자와 같다는 조건에 의해 아래와 같은 식(②, ③)이 나올 수 있습니다.
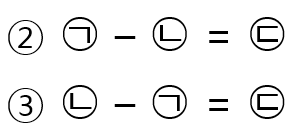
②번 식을 이용하여 ①번 식을 푸는 한 가지 방법(④)과 ③번 식을 이용하여 ①번 식을 푸는 또 다른 방법(⑤)이 있습니다.
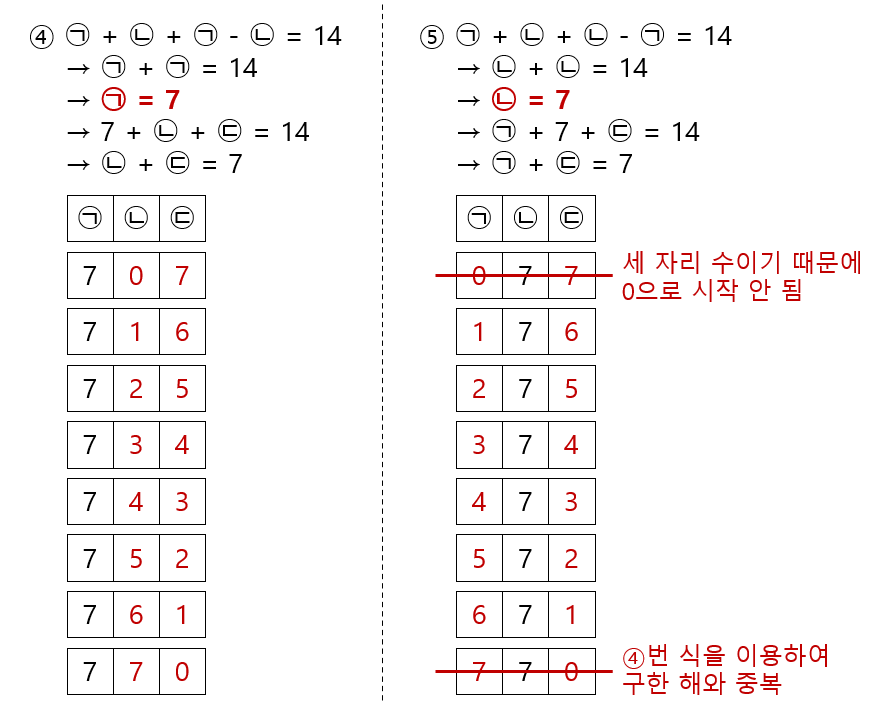
세 자리수는 모두 14개 입니다.
어려웠던 포인트
이 문제에서는 2가지 어려운 점이 있었던 것 같습니다.
1. "차"를 구하기 위한 방법을 ③번 식을 떠올리지 못 했습니다. ("차"에 대한 개념이 약했던 것 같습니다.)
2. 무엇보다 중요한 것은 문제로부터 식을 도출하는 것에 익숙하지 않았습니다.
앞으로 문제를 풀 때 식을 도출하는 것에 대해 중점을 두고 연습을 해야 할 것 같습니다.
3. 문제
다음과 같이 어떤 규칙에 따라 수가 나열된 표가 있습니다. 표 (6)에서 31의 바로 위의 수와 바로 아래의 수의 합은 얼마일까?
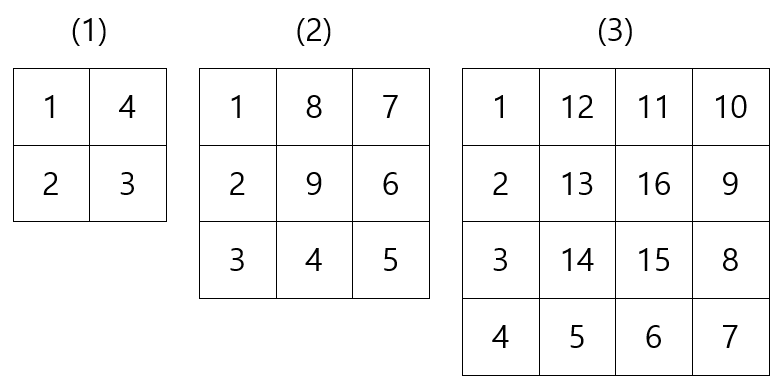
위 문제의 규칙은 아래와 같습니다.
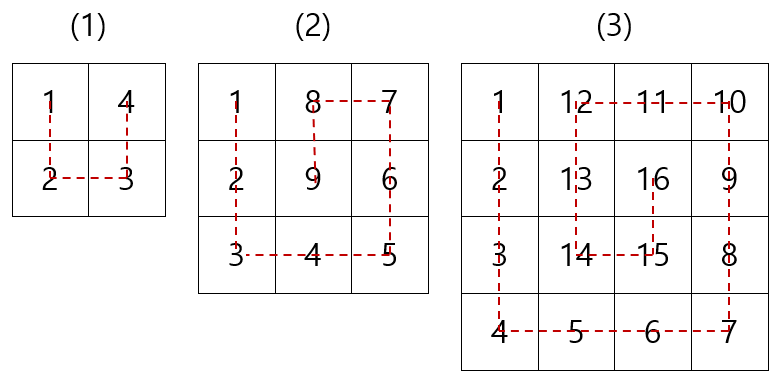
규칙에 따라 (6)까지 그려보면 아래와 같습니다.
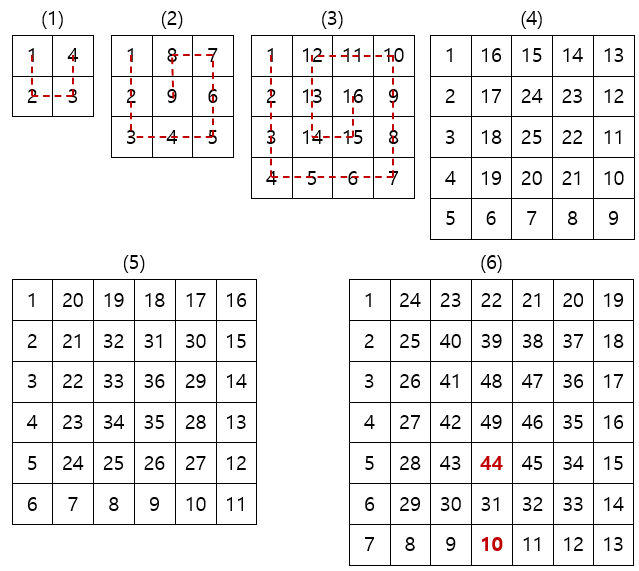
31 바로 위의 수는 44, 바로 아래 수는 10으로 두 수의 합은 54 입니다.
어려웠던 포인트
이 문제는 규칙을 못 찾았다고 아이가 말을 했는데, 문제를 풀었던 과정을 보면 아래 그림과 같이 규칙에 해당하는 선을 찾아서 표에 그려놓았었습니다.

틀린 문제를 바로 같이 풀지 않고, 아이 혼자 다시 풀어보고 다시 틀리거나 모르는 문제를 같이 보는데, 이 문제는 모르겠다고 했던 문제입니다. 앉아서 같이 풀면서 "이 규칙이 멀까?" 라고 물으니 "잘 모르겠어... 아!" 하면서 규칙을 바로 찾았습니다.
이렇게 혼자 풀 때는 못 푸는 문제들을 옆에 앉아 질문을 던지면 혼자 곰곰히 생각하다 문제를 푸는 경우들이 종종 있었던 것 같은데, 왜 그런지 잘 몰라 오답 노트에 남겨놓습니다.
아이 교육에 대해 관심 있으신 분들은 편하게 연락 또는 댓글 달아주세요.
'교육 > 수학' 카테고리의 다른 글
| [수학][시매쓰][기프티드] 랭퍼드 문제 (2) | 2024.04.27 |
|---|---|
| [수학][최상위] 파스칼의 삼각형 (10) | 2024.02.27 |
| [수학][오답노트] 성대 경시 27회 (22) | 2024.02.09 |
| [수학][오답 노트] 피보나치 수열 (4) | 2024.02.02 |
| [수학][경시] 성대 경시 접수 방법 (108) | 2024.01.28 |



