기프티드(G-2) 과정 숙제로 나온 문제 중 아이가 어렵다고 했던 문제가 있어 정리해봅니다.
목차
랭퍼드(Langford) 문제
문제를 알아보기에 앞서 랭퍼드 문제가 무엇인지 간단히 정리하고 시작하겠습니다.
랭퍼드 문제란?
Langford 문제는 흥미로운 수학 퍼즐로, 숫자를 특정한 규칙에 따라 배열하는 데서 시작됩니다. 이 문제는 1950년대에 수학자 C. Dudley Langford가 처음 소개했으며, 간단해 보이지만 생각보다 도전적인 면이 있습니다. 문제의 핵심은 각 숫자 1,2,3,...,n이 정확히 두 번씩 사용되며, 두 같은 숫자 사이에 그 숫자만큼의 숫자가 위치해야 한다는 것입니다. 예를 들어, 숫자 1 사이에는 1개의 숫자, 숫자 2 사이에는 2개의 숫자가 와야 합니다.
이 규칙을 따르면, n = 3의 경우는 다음과 같은 배열이 가능합니다.
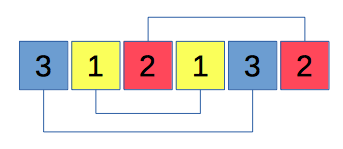
여기서 각 숫자 사이에 숫자의 값만큼 숫자들이 있습니다.
문제 및 풀이
Langford 문제는 앞에서 알아본 것과 같이 숫자 1부터 n까지 각각 두 번씩 나타나며, 두 숫자 k 사이에 정확히 k 개의 숫자가 오는 수열을 찾는 것을 말합니다. 이 문제는 수학에서 비교적 간단하게 설명할 수 있지만, 실제 수열을 찾는 것은 때때로 복잡할 수 있습니다. 특히n이 커질수록 수열을 찾기 어려워집니다.
이번 단락에서는 문제와 풀이과정에 대해 알아보겠습니다.
문제
312132는 1사이에 1개의 숫자가, 2사이에 2개의 숫자가, 그리고 3사이에 3개의 숫자가 있습니다. 일반적으로 1, ..., n이 각각 두 개씩 있을 때, 두 숫자 k사이에 k개의 숫자가 오는 수열을 만들 수 있는가 하는 문제를 Langford problem(랭퍼드문제)이라고 합니다. 312132는 n = 3에 대한 풀이입니다. 그렇다면 n = 4일 때의 풀이는 무엇일까요?
풀이과정
n = 4인 경우 다음과 같은 조건을 만족해야 합니다.
- 각 숫자 1부터 4까지가 두 번씩 나타나야 하며,
- 두 숫자 k 사이에 정확히 k개의 숫자가 있어야 합니다.
n=4일 때의 가능한 해답 중 하나는 다음과 같습니다.
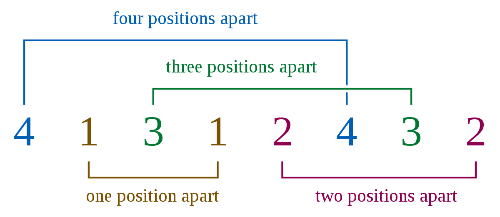
이 해답은 다음을 만족합니다:
- 1들 사이에는 1개의 숫자가 있습니다 (3).
- 2들 사이에는 2개의 숫자가 있습니다 (4, 3).
- 3들 사이에는 3개의 숫자가 있습니다 (1, 2, 4).
- 4들 사이에는 4개의 숫자가 있습니다 (1, 3, 1, 2).
n = 4에 대한 다른 해답은 하나만 있는 것은 아니고, 23421314 도 존재할 수 있습니다.
문제 풀이 참고
Langford 문제를 풀기 위해 n=4 경우를 구체적인 단계별로 설명하겠습니다.
1단계: 규칙 이해하기
- 각 숫자 1, 2, 3, 4가 두 번씩 나타나야 합니다.
- 숫자 k는 두 번째 등장까지 k개의 숫자가 있어야 합니다.
2단계: 수열의 길이 결정하기
- n = 4이므로, 수열의 총 길이는 2n = 8이 됩니다.
왜 2n인가?
각 숫자의 빈도: 문제의 규칙에 따라 숫자 1,2,3,...,n 각각이 두 번씩 나타나야 합니다. 즉, n개의 숫자 각각이 두 번 사용되므로 총 숫자의 개수는 n × 2 = 2n개가 됩니다.
3단계: 초기 배열 생성
- 8칸의 빈 배열을 만듭니다: [ , , , , , , , ]
4단계: 숫자 4 배치하기
- 숫자 4는 두 번째 4 사이에 정확히 4개의 숫자가 필요합니다.
- 배열의 끝 부분에서 충분한 공간을 고려하여 숫자 4를 배치해보세요.
- 예시: [ , , 4, , , , , 4]
5단계: 숫자 3 배치하기
- 숫자 3을 배열해보면서, 첫 번째 3과 두 번째 3 사이에 3개의 공간이 확보되는지 확인합니다.
- 예시: [ , 3, 4, , , 3, , 4]
6단계: 숫자 2 배치하기
- 숫자 2가 이제 두 번째 2 사이에 정확히 2개의 숫자를 포함하도록 배치합니다.
- 예시: [ 2, 3, 4, 2, , 3, , 4]
7단계: 숫자 1 배치하기
- 마지막으로 숫자 1을 두 번째 1 사이에 정확히 1개의 숫자가 오도록 배치합니다.
- 예시: [3, 1, 2, 4, 2, 3, 1, 4]
8단계: 결과 확인 및 검증
- 완성된 배열을 검토하여 모든 규칙이 만족되는지 확인합니다.
이 절차를 통해 n = 4인 경우의 Langford 문제의 해결책을 찾을 수 있습니다. 그러나 시행착오를 필요로 하며, 모든 n 값에 대해 해결책이 존재하는 것은 아닙니다. Langford 문제는 n이 1 또는 2를 제외하고는 n mod 4 = 0 또는 n mod 4 = 3인 경우에만 해결책이 존재합니다.
마무리
이전 글에서 "수학 잘하는 아이는 이렇게 공부합니다." 라는 책을 리뷰하였습니다.
[책 리뷰] 수학 잘하는 아이는 이렇게 공부합니다
자녀의 수학 학습 방법에 대해 고민하는 시점에 "수학 잘하는 아이는 이렇게 공부합니다"라는 책을 접하게 되었습니다. 고민했던 부분들을 잘 정리해놓은 책으로 내용을 정리해보았습니다. 목
wide-shallow.tistory.com
위 책에서는 문제해결력을 키우기 위해 다양한 방법으로 스스로 문제를 풀어봐야 하는 것을 강조했었는데, 어떠한 식을 통해 문제를 풀어가는 것이 아니라 시행착오를 통해 문제를 풀어가는 랭퍼드 문제는 문제해결력을 키우기 좋은 문제 유형이 라는 생각이 드네요.
'교육 > 수학' 카테고리의 다른 글
| [수학][씨매스][기프티드] 계단 오르기 문제 (0) | 2025.01.18 |
|---|---|
| [수학][씨매스][기프티드] 징검다리 문제 (0) | 2025.01.17 |
| [수학][최상위] 파스칼의 삼각형 (10) | 2024.02.27 |
| [수학][오답노트] 성대 경시 29회 (2) | 2024.02.12 |
| [수학][오답노트] 성대 경시 27회 (22) | 2024.02.09 |



